| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Transformer 디코더
- 셀프 어텐션
- 주간학습정리
- 어텐션
- 포지셔널 인코딩
- VAE 논문 리뷰 #
- self-attention
- 네이버 부스트캠프 AI Tech 6기
- seq2seq
- Transformer model
- 부스트캠프
- 어텐션 행렬
- 네이버 ai 부스트캠프
- VAE 설명
- 네이버 부스트캠프 AI Tech
- Positional Encoding
- pytorch
- Transformer 모델
- 네이버 부스트캠프
- 트랜스포머
- 트랜스포머 행렬
- VAE
- 네이버 부스트캠프 코딩테스트 후기
- AI Math
- 트랜스포머 모델
- 네이버 부스트캠프 KDT 전형
- Transformer Decoder
- transformer
- Auto-Encoding Variational Bayes
- boostcamp
- Today
- Total
DH. AI
VAE (Auto-Encoding Variational Bayes) 논문 리뷰 본문
디퓨전을 공부하기전에 VAE를 제대로 공부해보고 싶어서 정리한 글입니다.
Smart Design Lab 강남우 교수님의 강의를 보고 정리한 글입니다.
+ Boost Camp 강의도 조금 참고하였습니다. : 수정 1 2 3
VAE는 생성모델이다. Decoder부분을 만들어내기 위해서 Encoder부분이 필요하다.
VAE 논문에서 중요한 Contribution은 두가지이다.
1. 역전파가 되지 않는 단순 Sampling을 Reparameterization Trick을 사용하여 역전파가 가능하게 하였다.
2. Variational lower bound를 사용하여 interactable한 posterior의 근사치를 최적화 한다.
VAE 구조
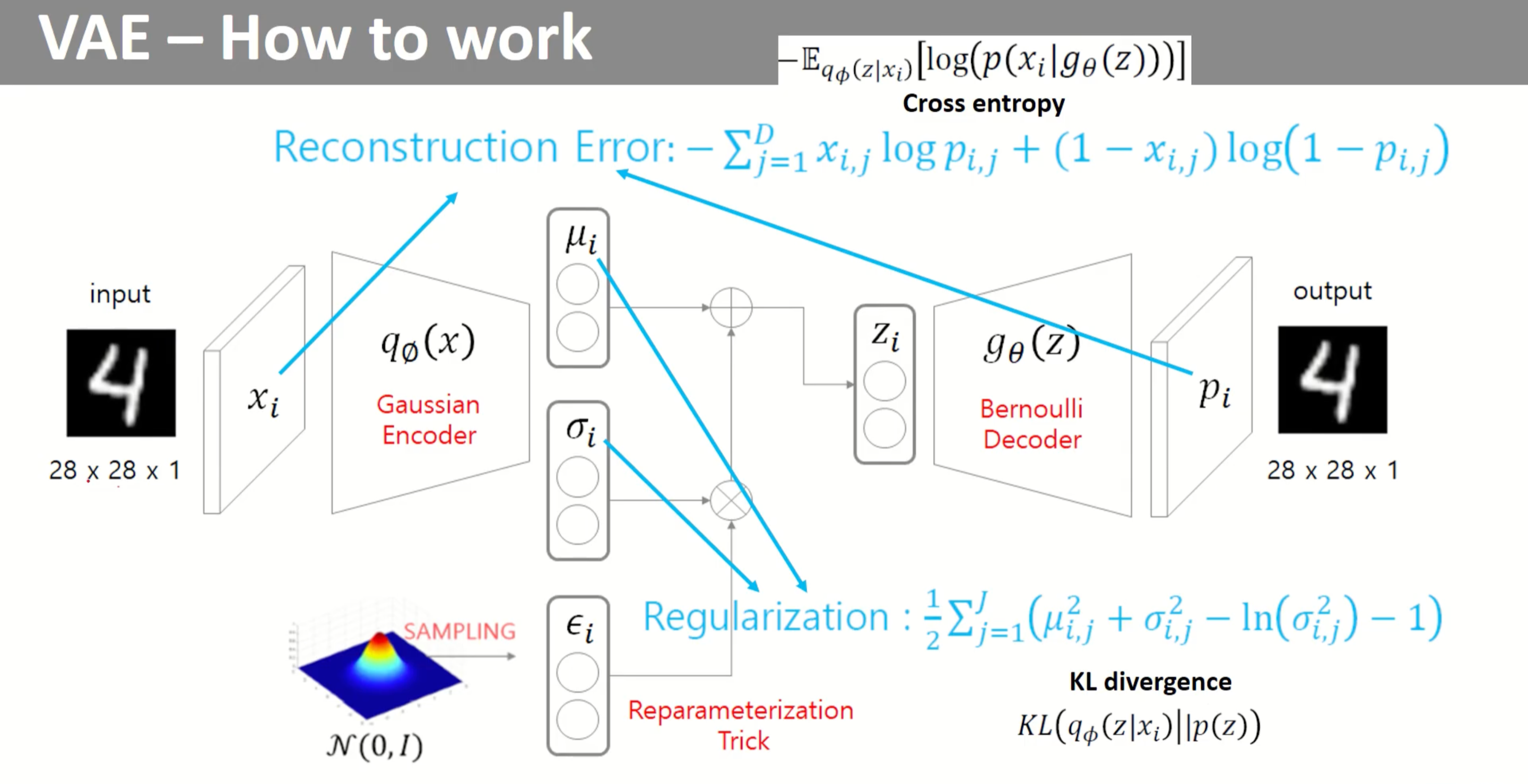
VAE의 전체적인 구조를 보면, 인코더 부분에서 𝜇(평균)와, 𝜎(분산)를 뽑아내게 된다.
이제 인코더의 결과를 통해서 출력된 𝜇, 𝜎 를 통해서 z를 뽑아내게 된다. 단순히 모수가 𝜇, 𝜎인 정규 분포에서 sampling하여 z를 만들어 내게 되면 역전파를 할 수 없으므로, 역전파가 가능하도록 Reparameterization Trick을 이용해 z를 구해내고, 평균과 분산으로 정규분포에서 z를 Sampling 한것과 같은 효과를 내게 한다. 이렇게 만든 Z를 디코더에 넣어 최종 Output을 만들어 낸다.
Loss는 두 부분으로 나눌 수 있다.

왼쪽이 Regularization, 오른쪽이 Reconstruction Error이다.
전체적인 구조를 파악했으니 어떻게 학습이 이루어지는 지 자세히 살펴보자!
∗ : true
Method
probolem scenario

목표!!! 가지고 있는 데이터 X가 나올 확률이 가장 커지는 확률분포를 찾고싶다. ( Maximize likelihood )
그냥 구하기엔 여러가지 문제점이 있더라.
아래 경우에도 효율적으로 작동하는 알고리즘을 원한다.
1. tractability : 위 상황에서 수식을 풀 수 가 없다.
(즉, posterior를 적분과 같은 계산을 통해서 구할 수 없는 경우에도 알고리즘이 작동해야 한다는 말이다. marginal likelihood의 적분식을 보면, 에 대해서 적분을 시행하게 되는데 우리는 에 대해서 알지 못하기 때문에 이를 실제 적분을 시행할 수 없다.)
2. A large dataset : 너무 많은 데이터를 가지고 있어서 batch optimization은 너무 연산량이 많다. 우리는 small minibatch나 심지어 하나의 datapoints만 사용해서 parameter update를 하고 싶다.
위의 시나리오에서 아래의 3개의 관련된 문제가 있다. 이에 대한 해결책을 제시한다.
1. Parameters 에 대한 Efficient approximate ML or MAP 추정
2. Parameter 의 선택을 위한 관측된 값 가 주어졌을 때 잠재 변수 에 대한 효율적인 approximate posterior inference.
3. 변수 의 효율적인 approximate marginal inference.
위의 문제들을 해결하기 위해, recognition model 를 도입한다. 이는 계산 불가능한 true posterior 에 대한 추정이다.
우리는 그러므로 recognition model 를 확률적 encoder로 지칭하며, 이는 datapoint 가 주어졌을 때 이 모델이 datapoint 가 생성될 수 있는 지점인 의 가능한 값들에 대한 분포(예를 들어, Gaussian 분포)를 만들어 내기 때문이다.
유사한 방식으로, 우리는 를 확률적 decoder로 지칭할 것이며, z(latent vector)가 주어졌을 때 이는 가능한 의 값들에 대한 분포를 만들어낸다. (Bernoulli, Gaussian 등)
아래에 제가 필기한 내용이 나오는데 알아보기 어려워도 양해부탁드립니다.. 😂
The Variational Bound
인코더를 도입하게 되면, likelihood는 다음과 같은 수식으로 유도 된다.
수정1 : 아래 수식 유도 시작부분에서 p(x)는 dose not depend on z 이기때문에 저런식으로 전개된다.
수정2 : 3번 은 줄이고 싶긴 함 (variational posterior와 true posterior 차이), 어차피 양수,true posterior를 계산할 수도 없음!! 따라서 그냥 ELBO(1번, 2번)만 최대화 하자!
수정3 : p(x)를 최대화 하고 싶은데 식을 전개 해서 보니, ELBO를 최대화 하면 3번(variational posterior와 true posterior 차이)은 줄어들고 p(x)는 최대화 할 수 있네..!? 라고 생각합니다.

위에서 구한 Variational lower bound를 최대화해야 하므로 -를 붙여 VAE Loss 를 정의한다.

위 확률 분포의 표현을 계산 가능한 식으로 변경시켜야 함. [ 참고 : p(x|gθ(z)) = pθ(x|z) ]
적은 수식을 깔끔한 이미지로 다시 가져오면...

Regularization부터 계산해보자.

다음으로 Reparameterization trick을 알아보고, Recontruction Error의 확률분포 표현을 풀어보자.

Recontruction Error
기대값의 표현을 적분 식으로 바꾸고, Monte-carlo technique를 사용한다. 하지만 L에 따라서 시간이 너무 오래 걸리기 때문에 L을 그냥 1로 두고 sampling을 한번만 해서 대표값을 사용한다.
Reparameterization Trick
위 그림과 같이 인코더에서 출력된 𝜇, 𝜎 를 사용하여, 단순히 모수가 𝜇, 𝜎인 정규 분포에서 sampling하여 z를 만들어 내게 되면 역전파를 할 수 없다. 즉, 이 파라미터들이 랜덤샘플링안에 섞여 있으면 Gradient 전달이 불가능하다. 따라서 모수가 0, 1인 정규분포에서 ϵ을 샘플링하여 z=μ+σϵ 수식으로 z를 만들어 낸다. 그렇게 되면 neural network를 통해서 역전파가 가능하다.
Recontruction Error의 확률분포 표현을 디코더의 확률분포 가정에 따라서 풀어보자.


앞의 과정에 따라서 Reconstruction Error와 Regularization이 수식화 되고, 위 그림처럼 일련의 학습이 진행된다. 결과적으로 z로부터 x를 만들어내는 Decoder를 학습 시켜 사용 할 수 있다.
VAE 특징
1. Decoder가 최소한 학습 데이터는 잘 생성 가능. - 생성된 데이터가 학습데이터와 좀 닮아 있음.
2. Encoder가 최소한 학습 데이터는 잘 latent vector로 표현 가능 - 데이터 추상화에 많이 쓰인다.
VAE 한계
1. intractable model이다. MLE로 출발하긴 했지만 근사를 통해서 최적화 하기 때문에 인코더, 디코더가 모두 확률분포라고 보기 어렵다.
2. 역전파를 해야하기 때문에 prior fitting term [p(z)]도 미분 가능해야한다. 따라서 많은 경우에 prior을 가우시안을 사용한다. 인코더도 정규분포! [q(z|x)]
'[딥러닝] > [Generative model]' 카테고리의 다른 글
| VAE (Auto-Encoding Variational Bayes) 코드 구현 (0) | 2023.03.13 |
|---|

